¿QUE ES UN CIRCUITO RL PARA CORRIENTE ALTERNA?
En la
parte de abajo de la página tienes un enlace a ejercicios resueltos en
corriente alterna, para que una vez estudiados puedes ver como se resuelven
este tipo de ejercicios.
Los receptores en corriente alterna
(c.a.) se pueden comportar de 3 formas diferentes.
Receptores Resistivos puros. Solo tienen resistencia pura. Se llaman
receptores R.
Receptores Inductivos puros. Solo tienen un componente inductivo puro (bobina).
Se llaman L.
Receptores Capacitivos puros. Solo tienen un componente capacitivo
(condensadores). Se llaman C.
En realidad no hay ningún receptor R,
L o C puro, ya que por ejemplo un motor eléctrico tiene un bobinado con
componente L, pero también esta bobina, por ser un cable, tiene una parte
resistiva, por lo tanto será un receptor RL o incluso si tiene una parte
capacitiva será receptor RLC.
Para analizar estos receptores en
circuitos, es mejor hacerlo de forma separada con su componente R, L y C
por separado. Así tenemos 3 tipos de circuitos, dependiendo el receptor.
Circuitos R, solo resistencia.
Circuitos L, solo bobina.
Circuito C, solo condensador.
Aunque como ya vimos los circuitos reales
serian RL, RC o RLC.
Vamos a estudiar como serían estos 3
circuitos por separado y luego veremos como serían los circuitos RL, RC y RLC.
CIRCUITOS R
Solo están compuesto con elementos
resistivos puros. En este caso la V y la I (tensión e intensidad) están en
fase, por lo que se tratan igual que en corriente continua. Esto en c.a. solo
pasa en circuitos puramente resistivos. En receptores resitivos puros la
impedancia es R.
CIRCUITOS
L
Son los circuitos que solo tienen
componente inductivo (bobinas puras). En este caso la V y la I están desfasadas
90º positivos. En estos circuitos en lugar de R tenemos Xl, impedancia
inductiva. L será la inductancia y se mide en henrios, al multiplicarla por w
(frecuencia angular) nos dará la impedancia inductiva . La Xl es algo así como
la resistencia de la parte inductiva.
CIRCUITOS C
Este tipo de circuitos son los que
solo tienen componentes capacitivos (condensadores puros). En este caso la V y
la I están desfasadas 90º negativos (la V está retrasada en lugar de adelantada
con respecto a la I).
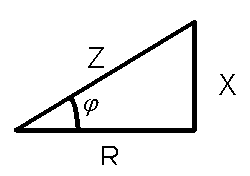
CIRCUITO RL EN SERIE
El circuito RL tiene un
componente resistivo y otro inductivo (R y L). Aquí partimos de la impedancia
que será un número complejo. El ángulo de desfase depende de la cantidad de
componente inductivo que tenga.
Z = R + Xlj , como Xl= w x L
(frecuencia angular por inductancia) podemos decir también Z = R + (w x L) j
CIRCUITO RC
Este es igual solo que ahora tenemos
Xc en lugar de Xl. Además Xc = 1/(wCj) y por lo tanto Z = R + 1/(wCj) en
numero complejo. Pero si hacemos el triangulo de impedancias en este caso la Z
en número natural sería:
Z2 = R2 + (1/(wC))2
CARACTERISTICAS
|
I
|
Intensidad
|
Amperios (A)
|
|
V
|
Tensión
|
Voltios (V)
|
|
f
|
Frecuencia
|
Hertzios (Hz)
|
|
L
|
Coeficiente de autoinducción,
(Inductancia)
|
Henrios (H)
|
|
w
|
Pulsación (velocidad angular)
|
radianes/sg
|
|
XL
|
Reactancia inductiva
|
Ohmios (W)
|
En el circuito de la figura
correspondiente se puede ver la resistencia y la bobina que son alimentadas por
la fuente de corriente alterna. También podemos apreciar el desfase existente
en caídas de tensión entre uno y otro componente. Debido a que las tensiones en
bornes de cada componente se pueden calcular, por la Ley de Ohm, aplicando que V
= I . R, y a que las intensidades que circulan por bobina y resistencia
están desfasadas entre sí 90 grados, la única forma de calcular la tensión
total que alimenta el circuito serie es aplicando la representación vectorial
que vemos en la figura y calculando con la fórmula pitagórica también indicada
el valor de VAC.
CIRCUITOS DE CORRIENTE ALTERNA
Estudiar
los circuitos en serie RL, RC y RLC en corriente alterna. Aplicación al cálculo
de L y C.
Alimentación de potencia: c.a. 6.3 V a 50 Hz. Voltímetro electrónico
(c.a. 0-10 V) u osciloscopio. Miliamperímetro (1 mA) Resistencias: 47 KQ
Condensadores: 470 nF. Autoinducciones: bobina de 8 H a 1 mA (aproximadamente).
Interruptor y cable de conexión.
FUNDAMENTO:
Cuando a Los extremos de una
resistencia óhmica se aplica una tensión alterna, V = VM sen w t, la intensidad de la corriente que
se origina se deduce a partir de la ley de Ohm:
resultando
que la intensidad también varía sinusoidalmente con el tiempo, con la misma
frecuencia que la tensión aplicada, y que su valor máximo vale
Por tanto, cuando un circuito sólo
contiene resistencia óhmica, la intensidad de la corriente no presenta
diferencia de fase respecto a la tensión aplicada que la origina (fig. 1).
En
general, en los circuitos de corriente alterna se suelen utilizar otros
elementos además de las resistencias óhmicas. Supongamos que existan,
conectadas en serie con una resistencia R, una bobina L y un
condensador C. Al aplicar una tensión alterna a los extremos de dicho
circuito en serie, se establece, una vez desaparecidos los efectos transitorios
de corta duración, una corriente estacionaria que viene expresada por
en
la que se pone claramente de manifiesto que la frecuencia f = w/2p de la intensidad es la misma que la
correspondiente a la tensión, pero que la intensidad está desfasada en un
ángulo f
(ángulo de desfase o desfase) respecto a la tensión.
Los
valores instantáneos de una intensidad de corriente, f.e.m. o diferencia de
potencial alternas, varían de un modo continuo desde un valor máximo en un
sentido, pasando por cero, hasta un valor máximo en el sentido opuesto, y así
sucesivamente. El comportamiento de un determinado circuito en serie queda
expresado por los valores máximos de la intensidad (Im) y de
la tensión (Vm) (también del valor del desfase φ), pero es
mucho más interesante estudiar los circuitos de corriente alterna en función de
los valores eficaces, lef y Vef,
en lugar de los valores máximos, porque los valores que se miden con los
voltímetros y amperímetros de c.a. son precisamente los eficaces.
La intensidad eficaz de una corriente alterna se define como el
valor de la intensidad de una corriente continua que desarrollase la misma
cantidad de calor en la misma resistencia y en el mismo tiempo. Se demuestra
que
y
análogamente, la tensión eficaz,
De
ahora en adelante, se interpretará que las letras I y V sin
subíndices hacen referencia a los valores eficaces de las magnitudes
correspondientes.
La
intensidad máxima Im está relacionada con la tensión máxima Vm
por una expresión que tiene la misma forma que la que expresa la ley de Ohm
para corrientes continuas
denominándose
la magnitud Z, impedancia del circuito, que es una generalización
de la resistencia R de la ley de Ohm en corriente continua.
Naturalmente, dividiendo los dos miembros de (6) por 
, se obtiene para los valores eficaces
La
relación que existe entre la impedancia Z del circuto RLC en serie y las
características R, L y C de los tres elementos
considerados es
que,
introduciendo las siguientes simplificaciones,
XL
= wL XC
= 1/wC X
= XL-XC
se
escribe
Por
otra parte, el desfase f, viene dado por la expresión
La magnitud X recibe el nombre
de reactancia; XL y XC son la reactancia
inductiva o inductancia y la reactancia capacitativa o capacitancia.
Tanto la impedancia como la reactancia se miden en ohmios (W).
Los papeles de la
inductancia y de la capacitancia son contrapuestos, tanto en lo que se refiere
a la limitación de la corriente, como al desfase que introducen entre la
intensidad y la tensión. Así, mientras que un aumento de inductancia reduce la
intensidad, un aumento de capacitancia la hace aumentar. Además, la inductancia
retrasa la intensidad respecto a la tensión, en tanto que la capacitancia la
adelanta. Tanto la inductancia como la capacitancia dependen de la frecuencia
de la tensión alterna aplicada.
La relación que existe entre la
impedancia Z de un circuito RLC en serie y los valores de R, XL
y XC puede representarse gráficamente considerando estas
magnitudes como vectores. La resistencia R se representa por un vector
situado sobre el eje Ox en sentido positivo del mismo; y las reactancias XL
y XC, por vectores situados sobre el eje Oy, en los sentidos
positivo y negativo, respectivamente. La impedancia Z será el vector
suma de los tres vectores. Véase la figura 2, denominada diagrama del vector
impedancia del circuito. En dicha figura, se ha considerado el caso en que
XL > XC, y por tanto X es positiva, y también
es positivo el desfase f.
Diremos que el circuito representado por dicho diagrama es
"inductivo". En el caso contrario, esto es XC > XL,
el circuito sería "capacitivo".
Como casos especiales, es evidente que
si el circuito sólo contiene una resistencia pura, entonces X = 0; Z = R y f = 0, y la intensidad está en fase con
la tensión aplicada.
Si el circuito contiene autoinducción
pura, será R = 0, Z = XL = wL y f = + p/2, y la intensidad se retrasa 90° respecto a la tensión
aplicada.
Pero si el circuito se compone de
capacidad pura, se tendrá R = 0, Z = XC = 1/wC y f = - p/2, y la intensidad adelanta en un ángulo de 90° a la
tensión.
La intensidad de la corriente tiene la
misma fase en todas las partes de un circuito en serie. Es decir: es máxima en
la resistencia, autoinducción y condensador al mismo tiempo; nula en los tres
un instante después; máxima, pero de sentido opuesto, otro instante todavía
posterior, y así sucesivamente.
La diferencia de
potencial (d.d.p.) entre dos puntos cualesquiera de un circuito es igual
al producto de la intensidad por la impedancia del mismo entre los dos puntos
considerados, siempre que no exista ninguna f.e.m. 
comprendida entre
dichos puntos. Así,
Vab=IZab
La diferencia de fase f entre Vab e I será f = arctg (Xab/Rab)
En la figura 4, la impedancia Zab
entre a y b es R y, por consiguiente, Vab = IR
y f = arctg0 = 0. Esto es, la d.d.p.
entre los terminales de una resistencia pura está en fase con la intensidad de
la corriente.
Entre los puntos b y c es Zbe
= XL, Vbe= IXL y f = arctg p/2. Esto es, la d.d.p. entre los
terminales de una autoinducción pura está adelantada 90° respecto a la
intensidad.
Entre los puntos c y d es Zed
= XC, Ved = IXC y f = arctg -p/2. Esto es, la d.d.p. entre los
terminales de una capacidad pura está retrasada 90° respecto a la intensidad.
Debido a estos desfases, la suma de la
diferencia de potenciales eficaces entre los extremos de un cierto número de
elementos de un circuito en serie no es igual a la diferencia de potencial
entre los extremos del conjunto. La suma de tensiones deberá efectuarse
geométricamente, como se indica en la figura 5, donde VR, VL
y VC son las tensiones entre los extremos de la resistencia R,
autoinducción L y capacidad C, respectivamente, y V es la
tensión entre los extremos de la asociación en serie RLC.
APLICACIONES DE CIRCUITO RL PARA CORRIENTE ALTERNA
- Se le
denomina corriente alterna a la que periódicamente cambia de sentido.Si la
frecuencia es de 60Hz, la dirección del movimiento de los electrones
cambia 120 veces por segundo. Estacorriente es la que se usa en casas, fábricas
y oficinas. Representa 90% de la que se consume en el mundo. Sirvepara las
mismas aplicaciones que la corriente continua, pero es mas fácil y barata
su transmisión, ya que comorecorre grandes distancias, puede enviarse a
voltajes de miles de cientos de volts y baja intensidad de corriente,
conlo que se pierde muy poca energía por calentamiento del conductor. Al
llegar a su destino solo se requiere que actuéun transformador para
reducir voltaje e incrementar su intensidad para que se aproveche en aparatos
domésticos ymaquinas industriales.
5. Z=/R2+XL2 I=E/Z IR=ER/R IL=EL/XLI=IR=IL E=/ER2+EL2
XL=2(pi)(F)(L)tanØ=XL/RZ Impedancia Ω ƒ Frecuencia HzL Inductancia Q Ø Angulo
de ° faseR Resistencia Ω I Intensidad de A corrienteXL Reactancia Ω E Tension
de V Inductiva corriente1H=(V)(s)/A 1H=(Ω)(s) 1Ω=V/A H=Henry V=Volt A=Ampere
Resistencia.
Según se discutió en el Apartado 2.3.2, en corriente continua la relación que
existía entre la caída de potencial V y la intensidad I en una resistencia
caracterizada por R venía dada por la ley de Ohm, esto es, V = RI.
Experimentalmente puede verificarse que la ley de Ohm sigue siendo válida para
corrientes alternas y, por tanto, I t( ) R V t( ) + - puede escribirse que1
I(t) = V (t) R . (5.2) Condensador. En la expresión (1.57) se definió la
capacidad C de un condensador como la relación entre la carga Q de las placas y
la caída de potencial V entre éstas, esto es, C = Q V . (5.3) Esta relación se
cumple igualmente para corrientes alternas, de donde puede deducirse que la
carga variable en el tiempo, Q(t), puede escribirse como Q(t) = CV (t) . (5.4)
Al derivar la expresión anterior respecto al tiempo obtenemos la siguiente
relación entre la intensidad I(t) y la caída de potencial entre las placas V
(t): I(t) = C dV (t) dt . (5.5) Esta relación indica que la derivada temporal
de la caída de poI t( ) V t( ) C + - tencial entre las placas está relacionada
linealmente mediante el parámetro C con la intensidad que llega al condensador.
Bobina. Tal y como se expresó en (4.42), el efecto de autoinducción
electromagnética de una bobina caracterizada por una inductancia L y recorrida
por una intensidad I(t) podía considerarse como una caída de potencial en la
bobina, V (t), dada por I t( ) V t( ) L + - V (t) = L dI(t) dt . (5.6) 1Los
signos más y menos en la resistencia y en otros elementos en los circuitos de
corriente alterna indican los puntos de potencial más alto y más bajo en dichos
elementos cuando la corriente tiene el sentido supuesto en la correspondiente
figura.
