CIRCUITO RL PARA CORRIENTE ALTERNA

CIRCUITO RL PARA CORRIENTE ALTERNA

CIRCUITO RL: Un circuito RL es un circuito eléctrico que contiene una resistencia y una bobina en serie. Se dice que la bobina se opone transitoriamente al establecimiento de una corriente en el circuito.

CARACTERÍSTICAS:  Los circuitos RL son aquellos que contienen una bobina (inductor) que tiene auto inductancia, esto quiere decir que evita cambios instantáneos en la corriente. Siempre se desprecia la auto inductancia en el circuito puesto que se considera mucho menor a la del inductor. Para un tiempo igual a cero, la corriente comenzará a crecer y el inductor producirá igualmente una fuerza electromotriz en sentido contrario, lo cual hará que la corriente no aumente. A esto se le conoce como fuerza contra electromotriz.

La reactancia inductiva se representa por y su valor viene dado por:

XL = WL = 2πFL

En la que:

XL= Reactancia inductiva en ohm
L= Inductancia en henrios
F= Frecuencia  en Hertz
W= Frecuencia angular

FUNCIONES:

Ley de tensiones de Kirchhoff: La suma de las tensiones en un lazo debe ser 0.

Ley de Ohm: La tensión en una resistencia es igual al producto del valor dicha resistencia por la corriente que fluye a través de ella.

Teorema de Norton: Cualquier red que tenga una fuente de tensión o de corriente y al menos una resistencia es equivalente a una fuente ideal de corriente en paralelo con una resistencia.

Teorema de Thévenin: Cualquier red que tenga una fuente de tensión o de corriente y al menos una resistencia es equivalente a una fuente ideal de tensión en serie con una resistencia.

APLICACIONES: El circuito RL tiene un componente resistivo y otro inductivo (R y L). Aquí partimos de la impedancia que será un número complejo. El ángulo de desfase depende de la cantidad de componente inductivo que tenga.

   Z = R + Xlj , como Xl= w x L  (frecuencia angular por inductancia) podemos decir también Z = R + (w x L) j

   Este número complejo lo podemos representar con el llamado triángulo de impedancia:



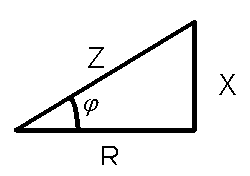
   En la imagen X sería Xl, si tuviéramos Xc (parte capacitiva), X sería (Xl-Xc). Según este triángulo podemos convertir el número complejo en número natural de la siguiente fórmula (por Pitágoras):

   Z² = R² + Xl²    Podríamos despejar Z para calcularla.

   La intensidad sería I = V / Z, que en instantánea quedaría:

   i = (Vo x seno wt) / (R + wLj) en complejo. Podemos convertirlo en eficaz sustituyendo la Z por la raíz cuadrada de (R + wL).

   Los valores eficaces seríán V = I /Z o I = V/Z.